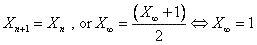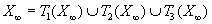IFS : definition
Iterated function systems, or IFS, are used to describe objects which are built by recursively applying a set of transforms on a set of sub-objects.
IFS can generate objects with self similarity properties, and objects with non integer
fractal dimensions.
There are various existing classes of IFS depending on the how objects and transforms are defined and on the set of rules used
to dictate how the transforms are applied to the objects.
L-Systems, subdivision surfaces and curves and many fractal objects are definable within an IFS frame.
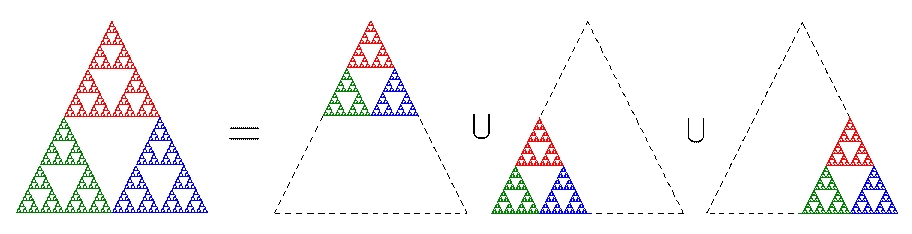
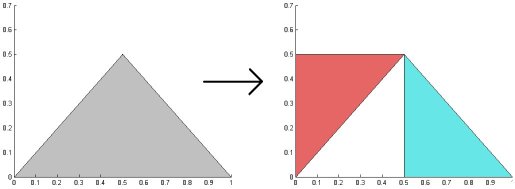
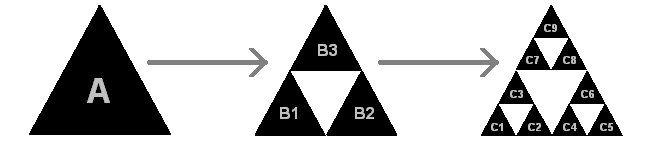
The Sierpinsky gasket is a famous and simple example of an object which can be described in terms of IFS.
A triangle gives birth to three similar triangles, each of which is obtained by applying a geometric transform (scaling, translation, rotation) on the parent triangle.
The three new triangles each give three other triangles by the same transforms, and so on recursively.
A few notions
Transformation trees
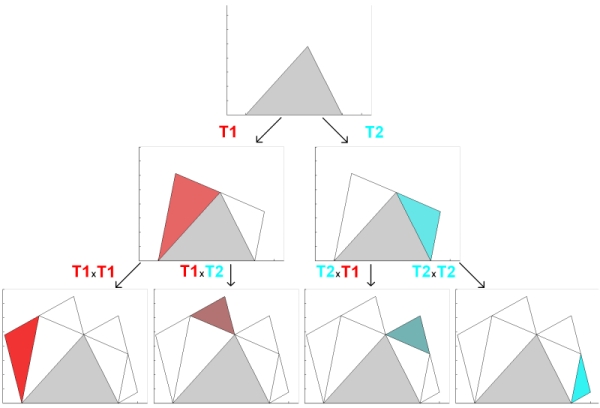
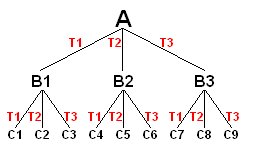
The triangle A in the previous figure can be considered as the root of a tree. Each following triangle is a node of this tree and branches linking nodes are transformations.
The tree reads as follows : Transformation T2 applied to triangle A gives level-2-triangle B2, and transformation T3 applied to B2 gives level-3-triangle C6.
The transformations defining the Sierpinsky gasket are :
T1 : scaling by factor ½.
T2 : scaling by factor ½ followed by translation B1->B2.
T3 : scaling by factor ½ followed by translation B1->B3.
One way to define transforms is by the expression of their matrices in homogenous coordinates.
Any node of the tree can be obtained by multiplying a series of matrices defining the address of this particular node
in the tree and applying the resulting transform to the root object.
IFS attractor and fixed point theorem
An IFS attractor is the limit towards which the set of leaves (terminal nodes) of the tree tends as you make more iteration.
Instead of using triangle objects and 3 transforms, consider a very simple IFS in which objects are real numbers and there is only one transform.
This transform, applied to a real number is: add one (a translation of 1 on the real axis) and divide by two (scaling of 1/2).
This transformation is very similar to the transformations in the Sierpinsky gasket example, but in a 1-dimensional space (the real axis).
From any root object, apply this transformation a few times and you will invariably tend toward a limit number :
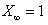
For example, from the root object 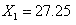 ,
you'll build the single branched tree:
,
you'll build the single branched tree:
The limit of this IFS, or fixed point, or  is the solution of the equation:
is the solution of the equation:
Similarly, the attractor of the Sierpinsky Gasket is the set of points which remains constant if you apply the IFS transforms to it.
The image of an attractor by the transformations of the corresponding IFS is itself.
For the Sierpinsky gasket, this means that the attractor is defined by :
where T1, T2 and T3 are the transforms previously defined.
The attractor is in whole similar to parts of itself. This is a property common in IFS attractors and fractal objetcs.
Attractor invariance
We built a very simple IFS defined on objects of the real axis in introduction of the previous paragraph on this page.
We stated that nomatter which real number we took as the root of our transformation tree, the leaf (terminal node) of the tree,
would unvariably tend toward the attractor : the number 1. Similarily, nomatter what object you take as root of the Sierpinsky gasket IFS
(for example, a square, a circle or a point), the attractor will remain constant.
This is illustrated in the following strip, where the transforms are recursively applied to squares.
Attractor approximation and chaos game
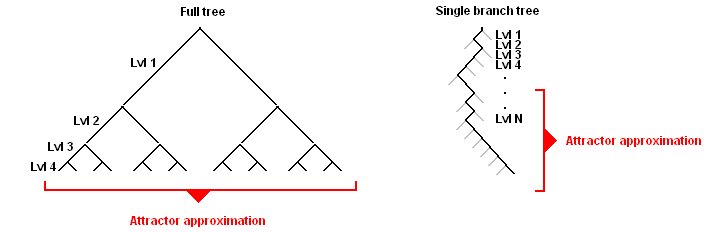
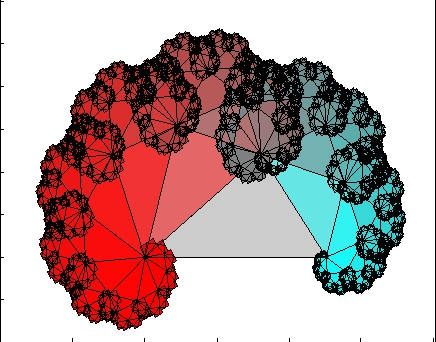
One way to approximate an IFS attractor is to iteratively apply all transforms to all objects defining a set of level N nodes of a tree
in order to build all level N+1 tree nodes, and repeat, as was done in the previous figure. This method is not always the most efficient method.
Another method is to pick a transform randomly to a single level N node object, apply this transform to create a single level N+1 node, and repeat.
The first method builds a complete level N tree, the leaves of which tend toward the attractor, the second method build a single branch tree of greater depth,
which tends toward the attractor. The second method is known as the chaos game.
More information on the game of chaos is available here.
Two other classic attractors
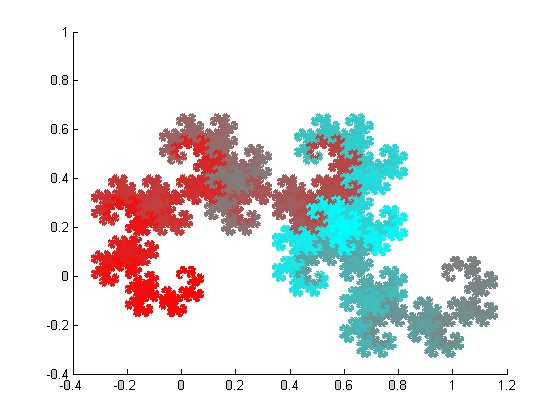
The dragon curve is defined by 2 transformations:
The building of a full level 16 tree, gives the following figures:
Pythagore trees are built in a similar manner, the two transforms are slightly different.
Here is a visualization of all the nodes of a level 12 tree. The approximation of the attractor of this particular IFS would be the leaves of this tree (smaller elements) :
Other famous attractors are very documented on the web, like the Barnsley fern, the Koch snowflake, the Sierpinsky carpet etc…
Links & ressources
There are plenty of things available on the web concearning IFS and fractals, among which :
Galleries of IFS structures I created.
A web page dedicated to a project I am working on, aiming to use IFS geometries in architecture, and more particularly in wooden structures.
A web page introducing fractals.
A web page describing the use of IFS and L-systems in the simulation of organic growth.
free software
In terms of free software, dedicated to the creation of IFS, I found these particularly nice and interesting :
LS Sketchbook creates L-Systems.
Apophysis creates non linear IFS.


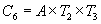
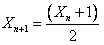
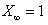
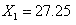 ,
you'll build the single branched tree:
,
you'll build the single branched tree: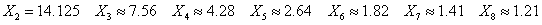
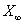 is the solution of the equation:
is the solution of the equation: